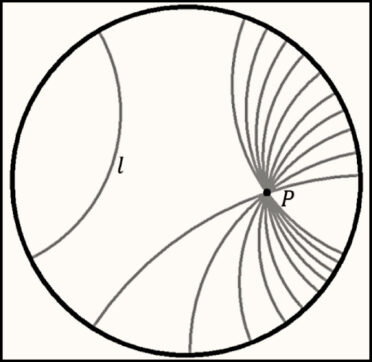
Soit une droite D. Soit un point P n’appartenant pas à la droite. Montrer qu’il existe une droite D’ et une seule passant par le point P et ne croisant pas D. Pas de panique, nous avons simplement construit deux droites parallèles dans un plan et, oui, selon l’axiome n°5 du grand Euclide d’Alexandrie, il existe en effet une unique droite passant par un point P et parallèle à une droite donnée. Une évidence résumée jadis à l’école primaire par la formule “deux droites parallèles ne se croisent jamais”. Tout est en ordre dans le meilleur des mondes géométriques, celui de notre perception quotidienne depuis l’Antiquité. Sauf que. Dans un article récent du collège de Clare à Cambridge, le mathématicien Maciej Dunajski explique comment « Circle LimitIV » de Maurits Cornelis Escher (ci-dessus), démonte l’évidence euclidienne. En géométrie hyperbolique, et eschérienne, donc, il existe une infinité de droites en question.
Certes, le peintre, dessinateur et graveur M.C. Escher (1898-1972) n’est pas l’inventeur des géométries non-euclidiennes, l’un des terrains de jeu favoris de la science des rapports et des mesures depuis des décennies. Mais sa démonstration dessinée en est sans doute l’une des plus élégantes. Et les mathématiciens ne s’y sont pas trompés, qui sont à leur tour venus à la rescousse du génie néerlandais de l’illusion graphique.
Après de longues tentatives pour essayer de défier les lois de la perspective en dessinant une image à répétition infinie, Escher avait ainsi décidé en 1956 de laisser vide la partie centrale de son dessin « Galerie d’Estampes ». L’idée de départ était de zoomer tout en opérant une rotation dans l’image, afin d’y retrouver in fine le même motif à l’infini. Après avoir agrandi l’image par un facteur 22,58 et tourné dans le sens des aiguilles d’une montre d’un angle de 157,63 degrés, on devait ainsi, selon le maître, retomber sur l’image originale. Las, le zoom amenait irrémédiablement sur le bord de la zone inachevée, et non au centre. Impasse. Cinquante ans plus tard, une équipe de mathématiciens dirigée par Hendrik Lenstra et Bart de Smit, deux pointures de Berkeley et de l’université de Leyde aux Pays-Bas, parviennent à compléter le dessin, après plusieurs mois de recherche. Le rébus a été comblé en utilisant notamment les propriétés des surfaces de Riemann. Que nous n’exposerons pas ici, bien à regret. (1)
La Monnaie de Paris montre, semble-t-il pour la première fois dans la capitale, les deux dessins réunis, la version inachevée et l’exercice résolu de « Galerie d’Estampes ». Aux côtés de cette curiosité légendaire, l’étendue et la qualité des œuvres présentées sont remarquables, probablement historiques à Paris. « De Jour et Nuit » (1938) à « Serpents », sa dernière gravure sur bois (1969), en passant par les panneaux spectaculaires de « Métamorphose II » (1939-40) l’organisateur, la société italienne Arthemisia, a réuni plusieurs des œuvres emblématiques de l’artiste.
Et la richesse de l’exposition se double d’une mise en scène accrocheuse. L’immersion du visiteur dans la salle « Es-tu vraiment sûr qu’un sol ne peut pas être aussi un plafond », donne vertigineusement le sentiment de l’infini. La « relativity room » est à parcourir avec un ami, qui revoit de manière amusante l’impression de taille et de distance. L’animation vidéo de ce qui est sans doute le plus célèbre motif d’Escher « Relativité », où des personnages se croisent sans jamais pouvoir se rejoindre, dans des escaliers situés dans différents espaces, est sans doute l’un des clous de l’expo. Le metteur en scène, l’opérateur de spectacles Fever, a eu l’idée d’y introduire des héros de films (de la « Nuit au musée », par exemple) ou des personnages de la culture pop (David Bowie), ce qui colore d’une dimension ludique l’inquiétante étrangeté initiale de l’œuvre.
Au risque de dénaturer le propos ? La plateforme Fever, l’un des géants mondiaux de l’événementiel culturel, envisage son métier comme une mission, “démocratiser l’accès à la culture et au divertissement en offrant des expériences et événements uniques”. Grand-public et/mais unique ? Après tout, « seuls ceux qui tentent l’absurde atteindront l’impossible », professait M.C. Escher.
Jean Cedro
(1) Surfaces de Riemann
Informations pratiques: M.C. Escher à la Monnaie de Paris, du 15 novembre 2025 au 1er mars 2026. 11, quai de Conti, Paris 6e.
Source images: Monnaie de Paris
